How to make LLMs say true things

The following describes my method for making LLMs say true things and not untrue things. I call it a World Model, after the rationalist concept.

A World Model is an embeddings database filled with beliefs (chunks of declarative statements) with a confidence percentage that's computed using Bayes Theorem.

For example, a World Model may contain beliefs like:

- Evan loves AI (80%)
- Evan has a weak tongue (70%)
- Evan is very pale (75%)
- Evan eats curry (70%)
- Evan likes sushi (80%)

A new belief is added to the database with evidence. For example, a belief might be "Evan loves AI" and the evidence might be a chatlog in which Evan said "thanks I love you!" to AI.

When we add a belief for the first time, create a prior confidence using existing beliefs. Here's an example prompt:

Is this statement true?

Context:
- @evan has a weak tongue
- @evan is very pale

Belief:
@evan happily eats very spicy food

Answer (yes / no):

Then, we can look at the logits for "yes" or "no", and use that as our prior probability, P(Belief). In this case, it's 7%.

Next, we can calculate the rest the likelihoods P(Evidence | Belief) and P(Evidence | ~Belief), by looking at the evidence. Let's say the evidence is "@evan ordered the spicy tuna roll".

Then we can use another prompt to calculate the likelihoods, given that the belief is true, and given that the belief is false. We'll include other semantically similar beliefs in the prompt.

Here's a prompt that finds P(Evidence | Belief), which gives us a likelihood of 98%:

Evan happily eats very spicy food Evan likes sushi. Evan eats curry.

Would Evan order the spicy tuna roll? (Yes / No):

Here's a prompt that finds P(Evidence | ~Belief), which gives us a likelihood of 17%:

Evan avoids very spicy food. Evan likes sushi. Evan eats curry.

Would Evan order a spicy tuna roll? (Yes / No):

Then we can calculate the posterior probability P(Belief | Evidence) using Bayes Theorem:

P(Belief) = 0.07
P(~Belief) = 0.93
P(Evidence | Belief) = 0.98
P(Evidence | ~Belief) = 0.17
P(Evidence) = 0.07 * 0.98 + 0.93 * 0.17 = 0.2267
P(Belief | Evidence) = 0.07 * 0.98 / 0.2267 = 0.3026025584

In other words, if the LLM observed me eating a spicy tuna roll, it would go from a 7% confidence that I like spicy food to a 30% confidence that I like spicy food!

Since all the variables in bayes theorem use other beliefs, we implicitly create an assumption tree. For example, if the world model learns that "Evan has a weak tongue" or "Evan eats curry" is false, it can recompute all the dependent beliefs.

Every belief can thus justify itself and even write you a proof (example seen below).

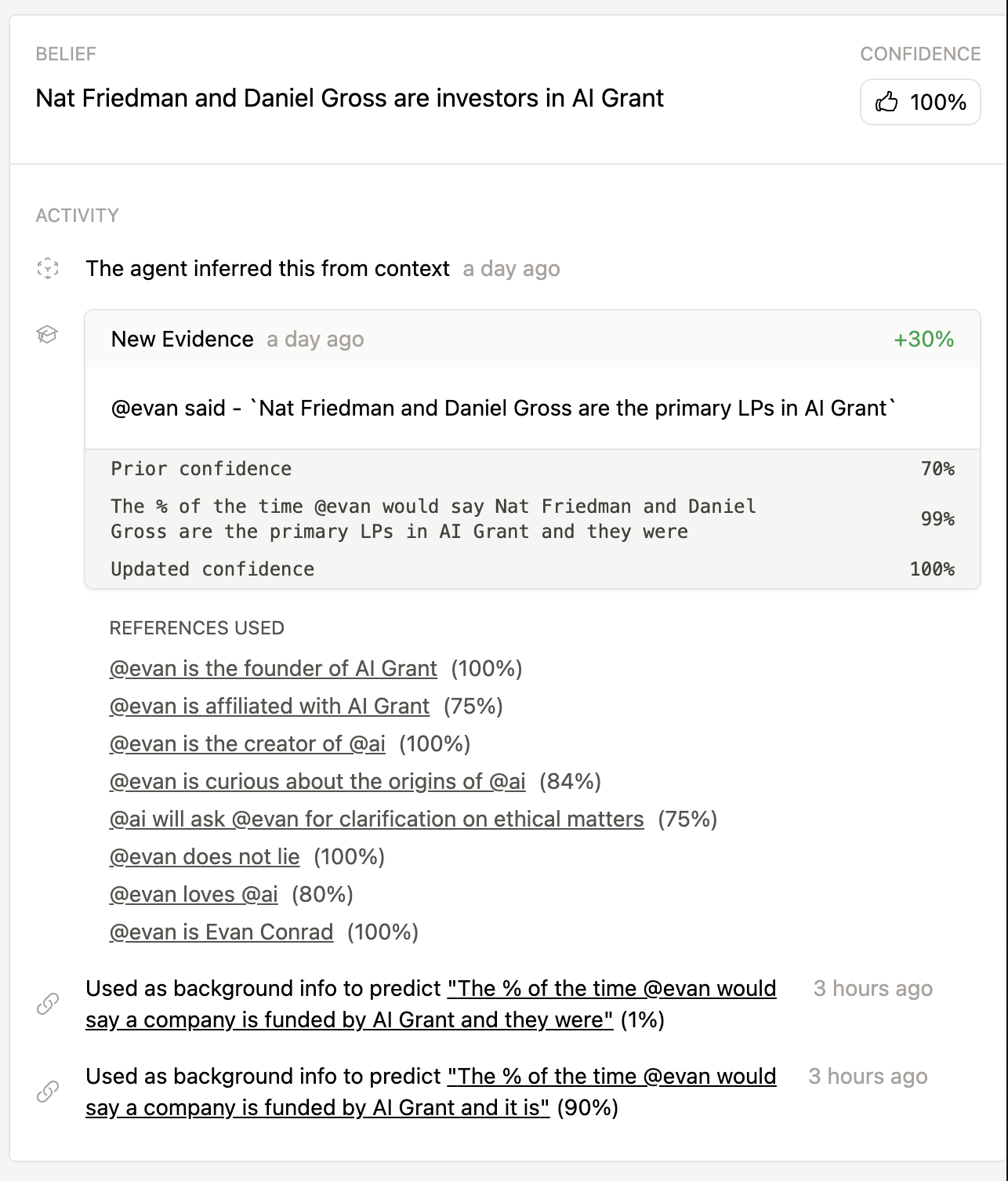
Limitations

• Overconfident likelihoods - Language models are over-confident and so your system for implementing it may want to be conservative. If the likelihood is 99%, you may want to set the confidence to 90% manually. (For example, in the screenshot above, the model is very confident I am the founder of AI Grant, when I definitely am not.)
• Trusting Sources - Some sources are not particularly trustworthy, and so your likelihood prompts may want to include context on why you trust (or don't trust) the source. For example, if you're using a chatlog, you may want to include the context of the conversation.